Cracking the Coding Interview: Q 3.4 Hanoi Tower Problem
Although the Hanoi Tower problem very basic, by studying it, we learn thinking in recursive way. Generally we should analysis the base cases and reorganize the problem into subproblems. The different thing from 4th edition is that, in 5th edition, it’s required to use stack to simulate the tower.
Question
In the classic problem of the Towers of Hanoi, you have 3 towers and N disks of different sizes which can slide onto any tower.The puzzle starts with disks sorted in ascending order of size from top to bottom (i.e., each disk sits on top of an even larger one).
You have the following constraints:
(1) Only one disk can be moved at a time.
(2) A disk is slid off the top of one tower onto the next tower.
(3) A disk can only be placed on top of a larger disk.
Write a program to move the disks from the first tower to the last using stacks.
Solution
First, let’s check the base case.
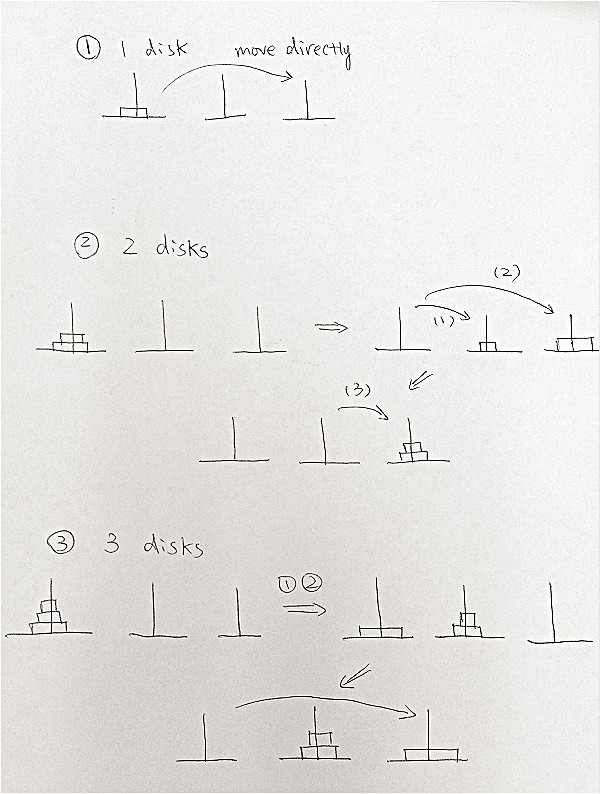
1. When only 1 disk
Move disk to destination tower directly. Nothing special.
2. When 2 disks
Move top disk onto middle tower and move larger disk onto destination tower. Then move small disk from middle tower to destination tower. Noticing that the middle tower is used as a buffer to store smaller disk. Because we always need to move largest disk onto destination when both source and destination towers have no smaller disks.
3. When 3 disks
From case 2 we know that we can move top 2 disks onto another tower in 3 steps, so here we move top 2 disks onto buffer tower. Then move largest disk onto destination. Repeat similiar 3 steps, 2 disks can be moved on to destination.
For last 3 steps, the buffer tower is changed. The source tower is used as a buffer.
4. When n disks (n >= 2)
Assume we need p steps to finish moving, at q step the situation is always like this:
n-1 disks on buffer tower, largest 1 disk on source tower. Then at q+1 step we move largest disk onto destination. The rest steps are used to move disks on buffer tower to destination.
So the problem is split into 3 parts.
(1) Move n-1 disks onto buffer tower.
(2) Move 1 largest disk onto destination tower.
(3) Move n-1 disks onto destination tower.
Clearly it’s a natural recursive algorithm. The implemetation is below. Notice that at different step diffrent tower is used as a buffer.
void Hanoi(stack<int>& from, stack<int>& buf, stack<int>& dest, int num) {
if (num == 0) {
return;
}
else if (num == 1) {
int temp = from.top();
from.pop();
dest.push(temp);
return;
}
else if (num == 2) {
int temp = from.top();
from.pop();
buf.push(temp);
temp = from.top();
from.pop();
dest.push(temp);
temp = buf.top();
buf.pop();
dest.push(temp);
return;
}
Hanoi(from, dest, buf, num-1);
Hanoi(from, buf, dest, 1);
Hanoi(buf, from, dest, num-1);
}The complete code is on GitHub.